Stone Landings
Introduction
The stability of stone cantilever staircases has been studied in recent years following collapses, the appearance of structural damage and general misunderstandings concerning how such structures work. It is now generally agreed the stair treads must interact with each other and only cantilever in the sense of torsional moments in supporting walls [ref Price & Myer 2005, Hume 2009 etc].
Attempts have been made to base assessment of cantilever stairs on Heyman’s Master Safe Theorem by lower bound limit analysis [ref], even though the structural actions depend on the ability of the stonework to transmit tensile stresses as well as compressive ones and to behave as a ductile material – which it isn’t, especially in tension!. The paper by Burgoyne et al (in preparation) intends to address this dilemma.
Little evidence has been found concerning the associated problems of explaining and analysing the structural actions and stability of stone landings. These are normally formed from separate slabs of stonework which interlock with each other and with supporting walls so as to transmit shear forces without significant normal moments. Although collapses are not known to have been reported, Ragsdale (2010) reported on defects in landings in Kedleston Hall which resulted in severe restraints on their use.
Such staircase structures are believed to be widespread, particularly in Georgian buildings in the UK, and similar period buildings throughout Europe including Italy from the time of Palladio? It thus seems an opportune moment to propose an account of how landings might work structurally supported by appropriate mathematical and numerical models and their verification and validation by physical tests.
A finite element model composed of plate bending elements governed by Reissner-Mindlin plate theory has recently been proposed. Each separate slab of a landing is modelled by a mesh of hybrid equilibrium elements. The meshes of adjacent slabs match their geometrical arrangements along the interfaces, and along the boundary segments of each mesh the normal and torsional components of moment are released and there is continuity only of transverse displacements.
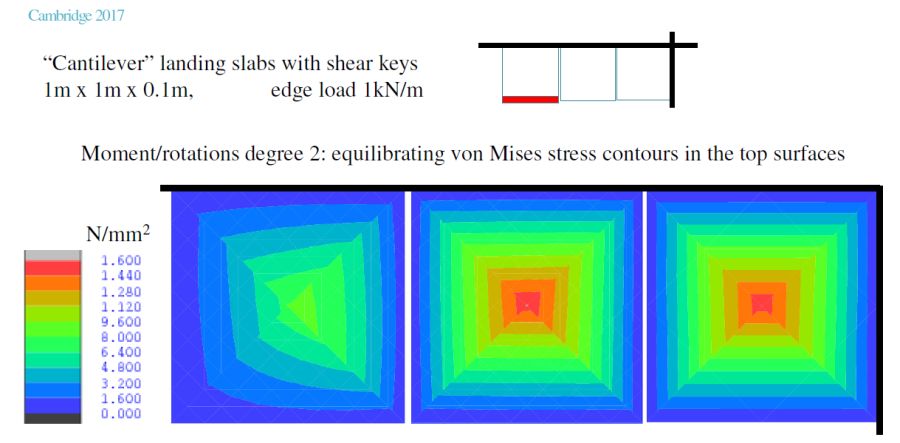
To date only a very simple model has been analysed assuming linear elastic behaviour. In this model each slab mesh is composed of four triangular elements of moment degree 2 and shear degree 1. This means that slab interactions involve only constant and linear distributions of shear force, which is the minimum degree of interaction required to demonstrate the overall stability of an arrangement of landing slabs, and the potential for defining hyperstatic fields of stress-resultants and their possible significance in the context of stability.
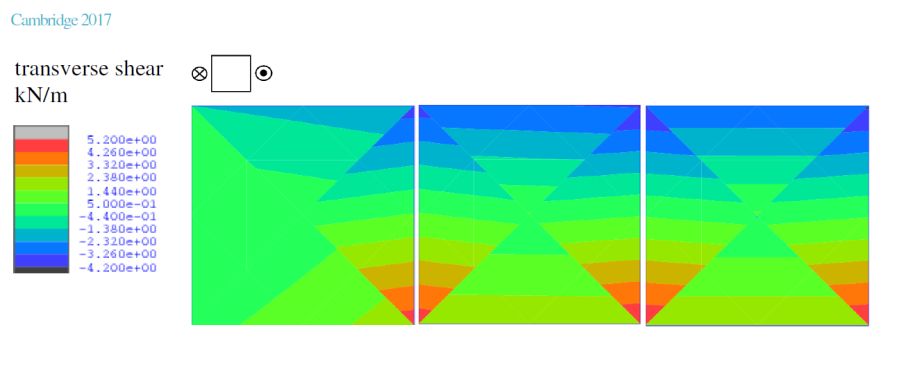
It is intended to explore the development of more refined models based on both p and h refinements, and also to investigate the use of lower bound limit analysis.
Team
Edward Maunder
Collaboration
Professor Chris Burgoyne
Paul Ragsdale
