Hyperstatic Stress Fields
Introduction
Hyperstatic stress fields are self-balancing stress fields found in structural members or mechanical components. They are self-balancing in the sense that they satisfy the relevant equations of equilibrium with zero body forces and boundary tractions. A classic example of hyperstatic stress field is that induced in a component subjected to a temperature field. The internal stresses are not zero but they are generated without the need for associated body forces or boundary tractions. Other examples include residual stresses due, for example, to manufacturing processes.
Hyperstatic stress fields are, though, more general than indicated above. Irrespective of the presence of thermally induced or residual stresses, they often exist quite normally within structural members or components as they are required, e.g., in a linear elastic structure, to ensure that the compatibility conditions are satisfied. In a plastic analysis, where compatibility conditions are no longer of importance, the hyperstatic stress fields are arranged so as to maximise the load carrying capacity of the member or component.
Hyperstatic Stress Field for a Plate Membrane Problem
A hyperstatic stress field for a plate membrane (planar elasticity) problem is shown in the following figure. The equations are used to define a set of equilibrating boundary tractions. Whilst statically admissible (SA), this stress field is not kinematically admissible (KA), i.e.,the corresponding strains do not satisfy the compatibility relations. The SA column plots the stresses given by the equations. The KA column is from a 2x2 mesh of compatible finite elements (CFE) model and so is kinematically admissible. The SAKA contours are from a highly refined CFE model. If the SA field is taken from the SAKA field then the hyperstatic stress required to make the SA field satisfy the compatibility relations is achieved.
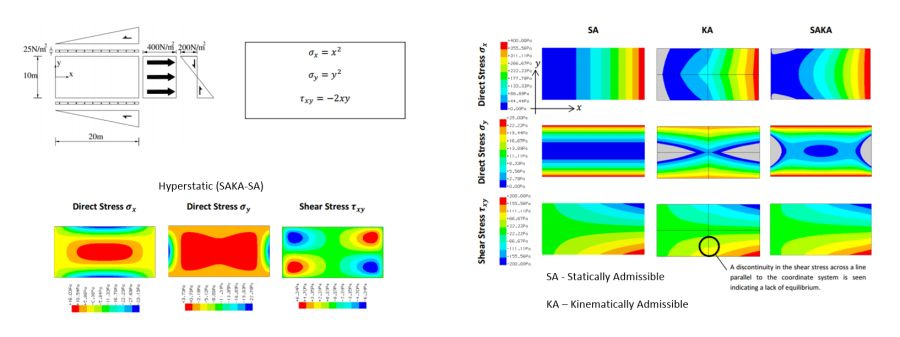
Whilst not the correct linear elastic stress field, the SA field has a useful property since, through the lower bound plasticity theorem, it may be used to provide a safe estimate of the ultimate limit state. Provided the stresses are kept within the relevant yield criterion then the structure is safe from plastic collapse. This property is utilised in Equilibrium Finite Element (EFE) analysis, which offers a useful alternative to conventional CFE analysis.
Hyperstatic Moment Field for a Kirchhoff Plate Bending Problem
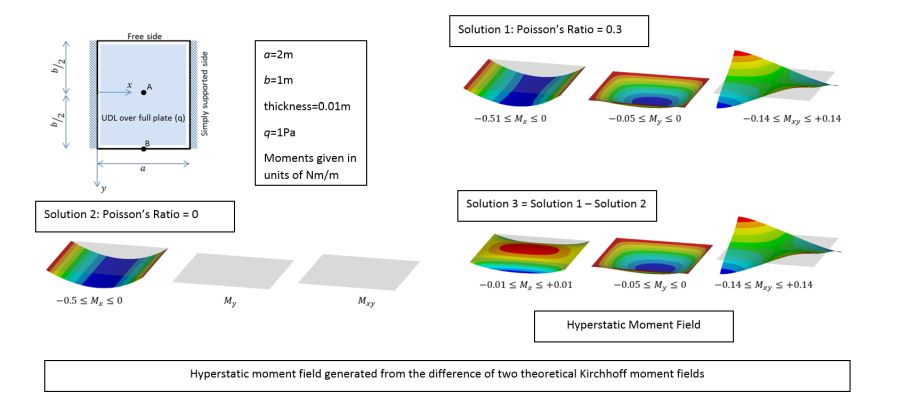
The solutions shown in the following figure are theoretical solutions for a Kirchhoff plate. The solution for zero Poisson's ratio is identical to that obtained from a beam solution - no transverse moments are generated. With Poisson's ratio equal to 0.3 then transverse moments are generated. The difference between solutions 1 and 2 is the hyperstatic moment field shown.
Hyperstatic Stress Resultants for a Beam Problem
In the third example of hyperstatic stress fields a statically indeterminate beam is considered. There are two hyperstatic stress resultant fields (bending moments and shear forces) which can be added to the particular solution in various combinations. The particular solution balances the applied load whereas the hyperstatic fields as, as usual, in equilibrium with no applied load.
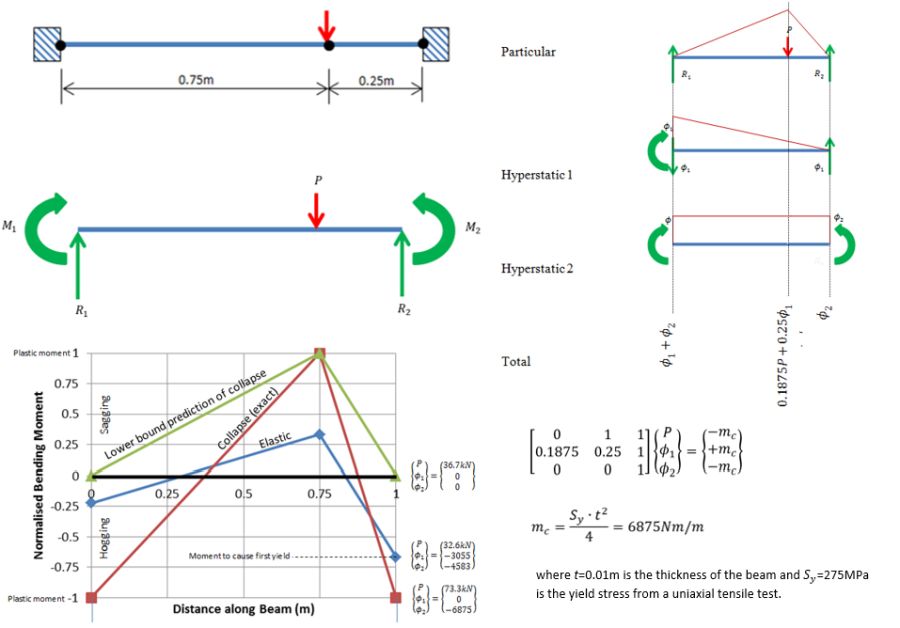
The normalised bending moment diagram (normalised by dividing by the plastic moment) shows three solutions, one of which is the elastic solution scaled so that the maximum moment just causes first yield. The amplitudes of the hyperstatic fields are those required to make the total solution satisfy the kinematic boundary conditions of zero rotation at both ends of the beam. If plastic hinges are allowed to develop then the applied load can be increased beyond that required to develop first yield. A lower bound prediction of collapse is shown where a plastic hinge has been allowed to develop under the load. The exact collapse load though is obtained when additional plastic hinges are allowed to develop at the supports.
Useful Links
Hyperstatic bending moment fields for a statically indeterminate beam (see figures 16 and 17)
Hyperstatic moment field for a Kirchhoff Plate (See Appendix)
Wikipedia: Stress-Strain Analysis
